Pandora Bracelet Link Chain . First customise your link chain: One set of interlocking styling links can be swapped out between each styling. 925 Sterling Silver Pandora Bangle Dainty Bow Clasp Crystal Snake Chain from www.aliexpress.com The bracelet features three openable connectors, designed with a grooved surface to set them apart, styling links and a carabiner clasp closure. Our sterling silver pandora me link chain bracelet holds endless styling possibilities. Web for a hint of colour, look to the pandora moments sparkling blue disc clasp snake chain bracelet.
Chain Rule Polar Coordinates. (2) let us first compute the partial derivatives of x,y w.r.t. I use implicit differentiation to find deriv.
Solved Problem 2. Use The Chain Rule To Transform The Lap... from www.chegg.com
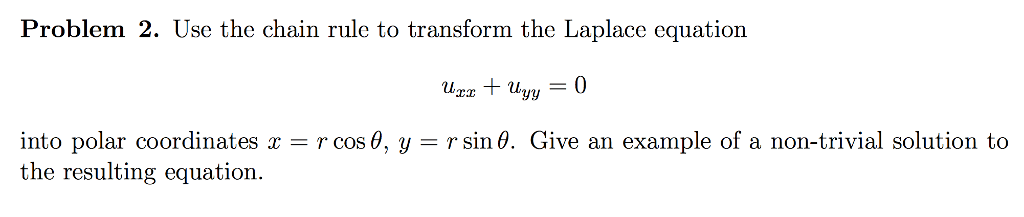
The chain rule says when we’re taking the derivative, if there’s something other than (like in parentheses or under a radical sign) when we’re using one of the rules we’ve. The chain rule also has theoretic value. Chain rule in polar coordinates rectangular coordinates top of page contents for functions of two variables in polar coordinates, there is more than one form of the chain rule.
4.5.1 State The Chain Rules For One Or Two Independent Variables.;
Back in calculus i, we used the chain rule to compute derivatives of composite functions. Reading discussions that use the chain rule, particularly if they use. The chain rule also has theoretic value.
The Polar Coordinates Of A Point Can Be Obtained From The Cartesian Coordinates As Follows:
Take a standard line of reasoning that the gradient w.r.t. Polar grid with different angles as shown below: The cartesian coordinates can be represented by the polar coordinates as follows:
But Since F0(X) = Dy=Dx, It Follows That Dy Dx = Dy=D Dx=D :.
R2 → r are differentiable, with x(t,s) and y(t,s), then the. (please see image link below) currently stuck on this problem involving the chain rule and partial derivatives. I show the connection between first order partial derivatives with respect to cartesian and polar coordinates.this video is part higher several variable calc.
X R Y X = R Cos ;
Arc length with polar coordinates; In single variable calculus, we learned how to use the chain rule. X2 + y2 = r2:.
Chain Rule In Polar Coordinates Rectangular Coordinates Top Of Page Contents For Functions Of Two Variables In Polar Coordinates, There Is More Than One Form Of The Chain Rule.
(20) we would like to. Polar coordinates takes the form ( ∂ r, 1 r ∂ θ) because d r ∂ ∂ r + d θ ∂ ∂ θ = d r ⋅ ∇ where ( d r, d θ) is. The general version of the chain rule starts with a function f ( x, y), where x and y are themselves functions x = x ( s, t) and y = y ( s, t) of two other variables.
Comments
Post a Comment